The way of the program
The goal of this book is to teach you to think like a computer scientist. This way of thinking combines some of the best features of mathematics, engineering, and natural science. Like mathematicians, computer scientists use formal languages to denote ideas (specifically computations). Like engineers, they design things, assembling components into systems and evaluating tradeoffs among alternatives. Like scientists, they observe the behavior of complex systems, form hypotheses, and test predictions.
The single most important skill for a computer scientist is problem solving. Problem solving means the ability to formulate problems, think creatively about solutions, and express a solution clearly and accurately. As it turns out, the process of learning to program is an excellent opportunity to practice problem-solving skills. That’s why this chapter is called, The way of the program.
On one level, you will be learning to program, a useful skill by itself. On another level, you will use programming as a means to an end. As we go along, that end will become clearer.
The Javascript programming language
The programming language you will be learning is Javascript. Javascript is an example of a high-level language; other high-level languages you might have heard of are Python, C++, PHP, Pascal, C#, and Java. It’s important to point out that Java and Javascript are two different programming languages with different syntax, styles, purposes, and histories. They unfortunately, share a very close name!
As you might infer from the name high-level language, there are also low-level languages, sometimes referred to as machine languages or assembly languages. Loosely speaking, computers can only execute programs written in low-level languages. Thus, programs written in a high-level language have to be translated into something more suitable before they can run.
Almost all programs are written in high-level languages because of their advantages. It is much easier to program in a high-level language so programs take less time to write, they are shorter and easier to read, and they are more likely to be correct. Second, high-level languages are portable, meaning that they can run on different kinds of computers with few or no modifications.
The engine that translates and runs Javascript is called the Javascript Interpreter. All modern web browser (Firefox, Chrome, Safari, MS Edge/IE, etc) ship with a Javascript interpreter. You can also install a stand-alone interpreter on your computer.
The longer code examples in this book will use Repl.it, an online programming platform and community. Code listings include links to the “repl” that you can copy (“fork”) and experiment with.
There are two ways to use the interpreter: interactive or immediate mode and script mode. In immediate mode, you type Javascript expressions into the interpreter’s console, and the interpreter immediately shows the result. This is the an example of the repl.it interpreter’s console:
The 2+2 is entered at the Javascript prompt. The ⠕ token indicates a statement entered at the prompt. The interpreter uses the prompt to indicate that it is ready for instructions. We typed 2 + 2 and hit enter the interpreter evaluated our expression, and replied 4, and on the next line it gave a new prompt. In this case, 4 is the output and it is indicated as output in our console by the => token.
Alternatively, you can write a program in a file and use the interpreter to execute the contents of the file. Such a file is called a script. Scripts have the advantage that they can be saved to disk, printed, shared, and so on.
For example, we created a file named main.js using our text editor. By convention, files that contain Javascript programs have names that end with .js, but they are just plain-text files.
To execute the program in repl.it, we simply click the “run” button. The output is shown in the console.
Working directly in the interpreter is convenient for testing short bits of code because you get immediate feedback. Think of it as scratch paper used to help you work out problems. Anything longer than a few lines should be put into a script.
What is a program?
A program is a sequence of instructions that specifies how to perform a computation. The computation might be something mathematical, such as solving a system of equations or finding the roots of a polynomial, but it can also be a symbolic computation, such as searching and replacing text in a document or (strangely enough) compiling a program.
The details look different in different languages, but a few basic instructions appear in just about every language:
- input
Get data from the keyboard, a file, or some other device.
- output
Display data on the screen or send data to a file or other device.
- math
Perform basic mathematical operations like addition and multiplication.
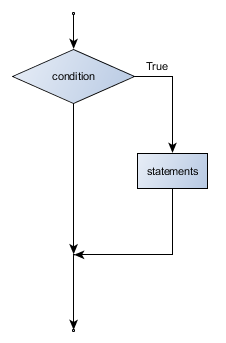
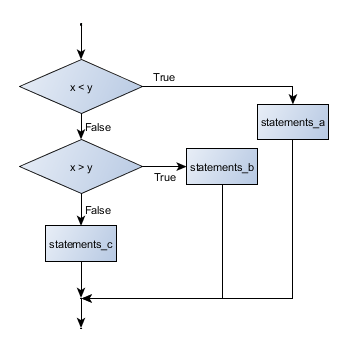
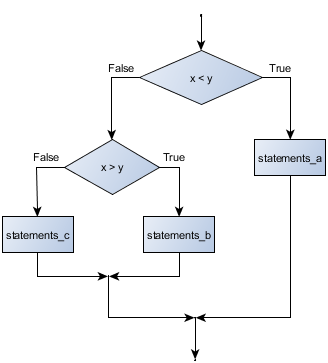
- conditional execution
Check for certain conditions and execute the appropriate sequence of statements.
- repetition
Perform some action repeatedly, usually with some variation.
Believe it or not, that’s pretty much all there is to it. Every program you’ve ever used, no matter how complicated, is made up of instructions that look more or less like these. Thus, we can describe programming as the process of breaking a large, complex task into smaller and smaller subtasks until the subtasks are simple enough to be performed with sequences of these basic instructions.
That may be a little vague, but we will come back to this topic later when we talk about algorithms.
What is debugging?
Programming is a complex process, and because it is done by human beings, it often leads to errors. Programming errors are called bugs and the process of tracking them down and correcting them is called debugging. Use of the term bug to describe small engineering difficulties dates back to at least 1889, when Thomas Edison had a bug with his phonograph.
Three kinds of errors can occur in a program: syntax errors, runtime errors, and semantic errors. It is useful to distinguish between them in order to track them down more quickly.
Syntax errors
Javascript can only execute a program if the program is syntactically correct; otherwise, the process fails and returns an error message. Syntax refers to the structure of a program and the rules about that structure. For example, in English, a sentence must begin with a capital letter and end with a period. this sentence contains a syntax error. So does this one
For most readers, a few syntax errors are not a significant problem, which is why we can read the poetry of E. E. Cummings without (too many) problems. Javascript is not so forgiving. If there is a single syntax error anywhere in your program, Javascript will display an error message and quit, and you will not be able to run your program. During the first few weeks of your programming career, you will probably spend a lot of time tracking down syntax errors. As you gain experience, though, you will make fewer errors and find them faster.
Runtime errors
The second type of error is a runtime error, so called because the error does not appear until you run the program. These errors are also called exceptions because they usually indicate that something exceptional (and bad) has happened.
Runtime errors are rare in the simple programs you will see in the first few chapters, so it might be a while before you encounter one.
Semantic errors
The third type of error is the semantic error. If there is a semantic error in your program, it will run successfully, in the sense that the computer will not generate any error messages, but it will not do the right thing. It will do something else. Specifically, it will do what you told it to do.
The problem is that the program you wrote is not the program you wanted to write. The meaning of the program (its semantics) is wrong. Identifying semantic errors can be tricky because it requires you to work backward by looking at the output of the program and trying to figure out what it is doing.
Experimental debugging
One of the most important skills you will acquire is debugging. Although it can be frustrating, debugging is one of the most intellectually rich, challenging, and interesting parts of programming.
In some ways, debugging is like detective work. You are confronted with clues, and you have to infer the processes and events that led to the results you see.
Debugging is also like an experimental science. Once you have an idea what is going wrong, you modify your program and try again. If your hypothesis was correct, then you can predict the result of the modification, and you take a step closer to a working program. If your hypothesis was wrong, you have to come up with a new one. As Sherlock Holmes pointed out, When you have eliminated the impossible, whatever remains, however improbable, must be the truth. (A. Conan Doyle, The Sign of Four)
For some people, programming and debugging are the same thing. That is, programming is the process of gradually debugging a program until it does what you want. The idea is that you should start with a program that does something and make small modifications, debugging them as you go, so that you always have a working program.
For example, Linux is an operating system kernel that contains millions of lines of code, but it started out as a simple program Linus Torvalds used to explore the Intel 80386 chip. According to Larry Greenfield, one of Linus’s earlier projects was a program that would switch between displaying AAAA and BBBB. This later evolved to Linux (The Linux Users’ Guide Beta Version 1).
Later chapters will make more suggestions about debugging and other programming practices.
Formal and natural languages
Natural languages are the languages that people speak, such as English, Spanish, and French. They were not designed by people (although people try to impose some order on them); they evolved naturally.
Formal languages are languages that are designed by people for specific applications. For example, the notation that mathematicians use is a formal language that is particularly good at denoting relationships among numbers and symbols. Chemists use a formal language to represent the chemical structure of molecules. And most importantly:
Programming languages are formal languages that have been designed to express computations.
Formal languages tend to have strict rules about syntax. For example, 3+3=6 is a syntactically correct mathematical statement, but 3=+6$ is not. H2O is a syntactically correct chemical name, but 2Zz is not.
Syntax rules come in two flavors, pertaining to tokens and structure. Tokens are the basic elements of the language, such as words, numbers, parentheses, commas, and so on. In Javascript, a statement like console.log("Happy New Year for ", 2013) has 6 tokens: a function name, an open parenthesis (round bracket), a string, a comma, a number, and a close parenthesis.
It is possible to make errors in the way one constructs tokens.
One of the problems with 3=+6$ is that $ is not a legal token in mathematics (at least as far as we know). Similarly, 2Zz is not a legal token in chemistry notation because there is no element with the abbreviation Zz.
The second type of syntax rule pertains to the structure of a statement—that is, the way the tokens are arranged. The statement 3=+6$ is structurally illegal because you can’t place a plus sign immediately after an equal sign. Similarly, molecular formulas have to have subscripts after the element name, not before. And in our Javascript example, if we omitted the comma, or if we changed the two parentheses around to say console.log)"Happy New Year for ",2013( our statement would still have six legal and valid tokens, but the structure is illegal.
When you read a sentence in English or a statement in a formal language, you have to figure out what the structure of the sentence is (although in a natural language you do this subconsciously). This process is called parsing.
For example, when you hear the sentence, “The other shoe fell”, you understand that the other shoe is the subject and fell is the verb. Once you have parsed a sentence, you can figure out what it means, or the semantics of the sentence. Assuming that you know what a shoe is and what it means to fall, you will understand the general implication of this sentence.
Although formal and natural languages have many features in common—tokens, structure, syntax, and semantics—there are many differences:
Glossary
- ambiguity
Natural languages are full of ambiguity, which people deal with by using contextual clues and other information. Formal languages are designed to be nearly or completely unambiguous, which means that any statement has exactly one meaning, regardless of context.
- redundancy
In order to make up for ambiguity and reduce misunderstandings, natural languages employ lots of redundancy. As a result, they are often verbose. Formal languages are less redundant and more concise.
- literalness
Formal languages mean exactly what they say. On the other hand, natural languages are full of idiom and metaphor. If someone says, “The other shoe fell”, there is probably no shoe and nothing falling.
You’ll need to find the original joke to understand the idiomatic meaning of the other shoe falling. Yahoo! Answers thinks it knows!
People who grow up speaking a natural language—everyone—often have a hard time adjusting to formal languages. In some ways, the difference between formal and natural language is like the difference between poetry and prose, but more so:
- poetry
Words are used for their sounds as well as for their meaning, and the whole poem together creates an effect or emotional response. Ambiguity is not only common but often deliberate.
- prose
The literal meaning of words is more important, and the structure contributes more meaning. Prose is more amenable to analysis than poetry but still often ambiguous.
- program
The meaning of a computer program is unambiguous and literal, and can be understood entirely by analysis of the tokens and structure.
Here are some suggestions for reading programs (and other formal languages). First, remember that formal languages are much more dense than natural languages, so it takes longer to read them. Also, the structure is very important, so it is usually not a good idea to read from top to bottom, left to right. Instead, learn to parse the program in your head, identifying the tokens and interpreting the structure. Finally, the details matter. Little things like spelling errors and bad punctuation, which you can get away with in natural languages, can make a big difference in a formal language.
The first program
Traditionally, the first program written in a new language is called Hello, World! because all it does is display the words, Hello, World! In Javascript, the script looks like this: (For scripts, we’ll show line numbers to the left of the Javascript statements.)
This is an example of using console.log, Javascript’s print function, which doesn’t actually print anything on paper. It displays a value on the screen’s console. In this case, the result shown is
The quotation marks in the program mark the beginning and end of the value; they don’t appear in the result.
Some people judge the quality of a programming language by the simplicity of the Hello, World! program. By this standard, Javascript does about as well as possible.
Turtle Graphics
In the late 1960s, Seymor Papert’s group at MIT introduced LOGO Turtle as a way to teach computer programming to kids. After learning the basic turtle commands (also called an API), you can make surprising computer graphics programs with only a little bit of code.
We’re using a version of Turtle that has been written for Javascript. Thanks to Morgan McGuire at Casual Effects for the code..
As we’ve seen, a program and algorithms consist of a number of commands or statements that execute in an order described by the program. There are many libraries or APIs (application programming interface) that help you useful do things in Javascript. Some APIsread files over a network, others choose random numbers, while others might encrypt data to make it more secure. The turtle API has a number of commands that you can use to move a turtle around a screen and to draw shapes and patterns.
Here’s a short turtle graphics program.
// set up the "pen" color and width
setWidth(30);
setColor("red");
// move forward 100px to draw a red line
fd(100);
wait(1);
// raise the pen "pen up -- pu()", then return the turtle
// to Y coordinate 0 and move it to X coordinate 100
pu();
setY(0);
setX(100)
pd();
wait(1);
// draw a blue line
setColor("blue");
fd(100);
wait(1);
// move turtle to the top left quadrant
pu();
setY(300);
setX(-300)
pd();
// draw a "DeepPink" circle
setColor("DeepPink");
startFill("DeepPink");
arc(360, 80);
endFill();
// hide the turtle
ht();
Run and remix this code on repl.it
Turtle programs use the metaphor of a turtle moving around drawing with a pen. To move the turtle without drawing, you call the “pen up” method, or pu(), as we do on lines 12 and 26. The turtle is plotted on an x,y plane (also called a Cartesian Plane). The x coordinate specifies the horizontal position of the turtle and the y coordinate specifies the vertical position of the turtle. In this plane, (0, 0) is in the middle of the window. Negative x coordinates are to the left of the center, and negative y coordinates are below the center. We call the setX() and setY() methods to move the turtle’s position. If the pen is down, it draws while we move. If it’s up, turtle moves without a trace. Notice how we draw a “DeepPink” circle, starting on line 32? Because our Javascript program executes in a web browser, we can use any of the “named colors” that are part of the web development standard. You can find all of the name colors here.
Turtle documentation
To fully use the turtle API, you will need to read and understand the documentation. Part of becoming a programmer and thinking like a computer scientist includes the ability to read (and write!) technical documentation. No programmer remembers every possible language feature or available commands. Before you begin the exercises and lab for this chapter, review the full
fd(distance)Move forward the given distance.
bk(distance)Move backward the given distance.
rt(angle)Turn right (clockwise) in place.
rt(angle, radius)Turn right (clockwise) in an arc of the given radius.
lt(angle)Turn left (counterclockwise) in place.
lt(angle, radius)Turn left (counterclockwise) in an arc of the given radius.
arc(angle, radius)Draw an arc around the turtle, without moving the turtle. The angle is relative to the current heading.
pu()Pick the pen up to temporarily move without drawing.
pd()Put the pen down to resume drawing.
ht()Hide the turtle.
setColor(color)Set the pen color by name such as RED or CSS color string such as “#FF0041”.
setColor(r, g, b)Set the pen color based on three RGB values each between zero and one.
setColor(r, g, b, a)Set the pen color based on three RGB values and an opacity value, each between zero and one.
startFill(color)Start drawing a filled region of the given color. Must end with
endFill()startFill(r, g, b)Start drawing a filled region with color given by three RGB values, each between zero and one.
setColor(r, g, b, a)Start drawing a region filled by three RGB values and an opacity value, each between zero and one.
endFill()End drawing a filled region and actually fill it. If the pen is down, then the outline will also be stroked.
setPosition(x, y)Sets the absolute position. If the pen is down, draws a line to that position.
setX(x)Sets the absolute x-axis position. If the pen is down, draws a line to that position.
getX()Returns the absolute x-axis position.
setY(x)Sets the absolute y-axis position. If the pen is down, draws a line to that position.
getY()Returns the absolute y-axis position.
setWidth(width)Sets the pen width.
setHeading(degrees)Sets the current heading in degrees measured clockwise from the upwards vertical axis. North = 0, East = 90, South = 180, West = 270.
getHeading()Returns the current heading in degrees measured clockwise from the upwards vertical axis. North = 0, East = 90, South = 180, West = 270.
setScale(s)Scales all distances (but not x and y coordinates or pen width) by this factor. Useful for reusing drawing commands for different size objects. 1.0 is the default scale.
getScale()Returns the current drawing scale.
setSpeed(speed)Sets the number of commands executed before showing the next frame of animation. Defaults to 1. Can be set to Infinity to draw the entire image at once. Does not affect wait times.
clear(color)Clears the screen to the specified color
clear(r, g, b)Clears the screen to the specified color
wait(seconds)Pauses drawing for approximately this many seconds. Useful for creating animations. Not affected by setSpeed.
Turtle Exercises 1
- Use
turtleto draw a red square with a pink border - Draw three circles, side-by-side. The first one should be blue, the second green, the third red.
- Draw a triangle.
- (bonus) Draw a 5-pointed star. Hint: draw this on a piece of paper first
First Turtle Lab
Our first lab presents an open-ended exercise, just to get you started. Use turtle graphics to draw a picture. We suggest you spend about one hour working on this lab. Make sure that you includes some commands from the documentation that are not in the example program. Other than that, the content of your drawing is up to you.
Glossary
- algorithm
A set of specific steps for solving a category of problems.
- bug
An error in a program.
- comment
Information in a program that is meant for other programmers (or anyone reading the source code) and has no effect on the execution of the program.
- debugging
The process of finding and removing any of the three kinds of programming errors.
- exception
Another name for a runtime error.
- formal language
Any one of the languages that people have designed for specific purposes, such as representing mathematical ideas or computer programs; all programming languages are formal languages.
- high-level language
A programming language like Javascript that is designed to be easy for humans to read and write.
- immediate mode
A style of using Javascript where we type expressions at the command prompt, and the results are shown immediately. Contrast with script, and see the entry under Javascript shell.
- interpreter
The engine that executes your Javascript scripts or expressions.
- low-level language
A programming language that is designed to be easy for a computer to execute; also called machine language or assembly language.
- natural language
Any one of the languages that people speak that evolved naturally.
- object code
The output of the compiler after it translates the program.
- parse
To examine a program and analyze the syntactic structure.
- portability
A property of a program that can run on more than one kind of computer.
- print function
A function used in a program or script that causes the Javascript interpreter to display a value on its output device.
- problem solving
The process of formulating a problem, finding a solution, and expressing the solution.
- program
a sequence of instructions that specifies to a computer actions and computations to be performed.
- Javascript console
An interactive user interface to the Javascript interpreter. The user of a Javascript shell types commands at the prompt, and presses the return key to send these commands immediately to the interpreter for processing.
- runtime error
An error that does not occur until the program has started to execute but that prevents the program from continuing.
- script
A program stored in a file (usually one that will be interpreted).
- semantic error
An error in a program that makes it do something other than what the programmer intended.
- semantics
The meaning of a program.
- source code
A program in a high-level language before being compiled.
- syntax
The structure of a program.
- syntax error
An error in a program that makes it impossible to parse — and therefore impossible to interpret.
- token
One of the basic elements of the syntactic structure of a program, analogous to a word in a natural language.





Comments
As programs get bigger and more complicated, they get more difficult to read. Formal languages are dense, and it is often difficult to look at a piece of code and figure out what it is doing, or why.
For this reason, it is a good idea to add notes to your programs to explain in natural language what the program is doing.
A comment in a computer program is text that is intended only for the human reader — it is completely ignored by the interpreter.
In Javascript, the
\\token starts a comment. The rest of the line is ignored. Here is a new version of Hello, World!.You’ll also notice that we’ve left a blank line in the program. Blank lines are also ignored by the interpreter, but comments and blank lines can make your programs much easier for humans to parse. Use them liberally!
Javascript also supports multiline comments with the
/* */style.In addition to adding hints and suggestions for human readers, comments play an important role in debugging. Because the Javascript interpreter doesn’t try to run commented lines, you can “comment out” sections of your code to isolate errors.
In the above code, only line 1 is interpreted and run as Javascript. The other lines are ignored. To debug this program, we can uncomment one line at a time until we find out which line has the buggy code.
It is so common for programmers to comment out large blocks of code when they are testing their programs, that programmer’s text editors support quickly commenting out sections of code. In repl.it, our online editor for this book, you can simply highlight the lines you want to comment or uncomment and use the Ctrl + / keyboard shortcut. You will see us using this technique in our example videos.